[LG Aimers] [지도학습-4] Classification

분류와 회귀의 차이

• 분류(Classification)
  • 출력이 이산적(유한한 값)
• 회귀(Regression)
  • 출력이 연속적(실수 값)

이진 분류

• 목표: 데이터를 두 그룹으로 분류
• 모델 설정:
  • 데이터셋 ${(x_i, y_i)}_{i=1}^n , y_i \in {0, 1}$
  • 함수 $f(x)$를 설정하고 손실 함수 $\mathcal{L}$ 최소화

• 0-1 손실 함수

  \[\mathcal{L}(y, \hat{y}) = \begin{cases} 0, & \text{if } y = \hat{y}, \\ 1, & \text{if } y \neq \hat{y}. \end{cases}\]
  • 문제점: 미분 불가능 → 다른 손실 함수 대안 필요

Perceptron 알고리즘

• 개념: 선형 분류기
• 장점:
  • 단순하며 선형적으로 구분 가능한 경우 수렴
• 단점:
  • 선형 분리가 불가능한 경우 무한 루프에 빠질 수 있음

서포트 벡터 머신(SVM)

• 핵심 아이디어:
  • 마진(margin): 결정 경계와 가장 가까운 데이터 포인트 사이의 거리
  • 최대 마진을 찾는 최적화 문제

  • $a^Tx+b=0$으로부터 포인트 $x_0$까지의 거리:

    \[d = \frac{|a^Tx_0+b|}{\|a\|}\]

• 최적화 문제:

  \[\min_a \frac{1}{2} \|a\|^2 \quad \text{subject to } y_i(a \cdot x^{(i)} + b) \geq 1\]
• 소프트 마진 SVM:

  • 오류 허용($\xi_i$): 슬랙 변수 추가

    \[\min_a \frac{1}{2} \|a\|^2 + C \sum_i \xi_i \quad \text{subject to } y_i(a \cdot x_i + b) \geq 1 - \xi_i\]

Hinge Loss

• 공식:

\[\mathcal{L}(y, f(x)) = \max(0, 1 - y \cdot f(x))\]

• 그러므로, 목적 함수는 다음과 같이 됨:

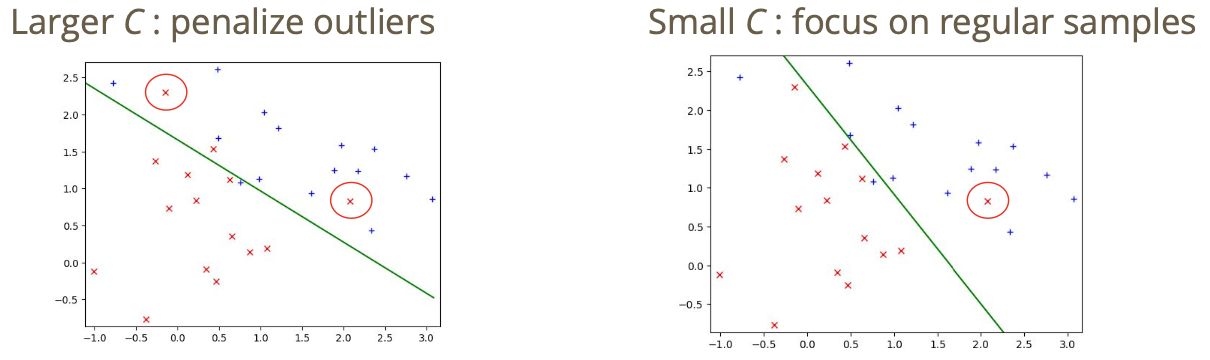
  \[\frac{1}{2}\|a\|^2 + C \sum_i \mathcal{L}(y_i, f(x_i))\]

• $C$ 값을 어떻게 설정하느냐에 따라서 결정 경계가 아래와 같이 달라지게 됨:

  

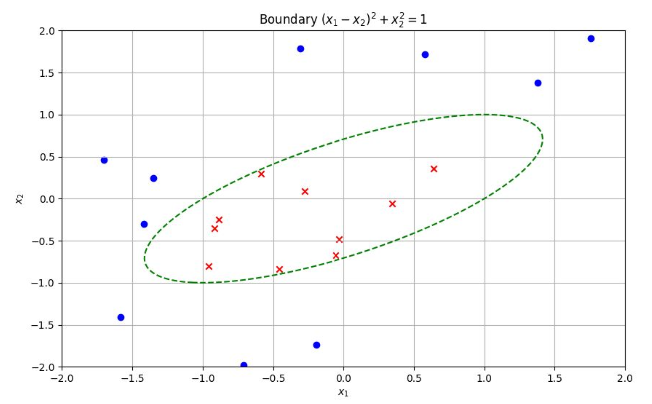
커널 기법

• 목표: 비선형 문제 해결
• 방법: 데이터의 특징 공간(feature space)을 확장

• 예) 다항 커널: