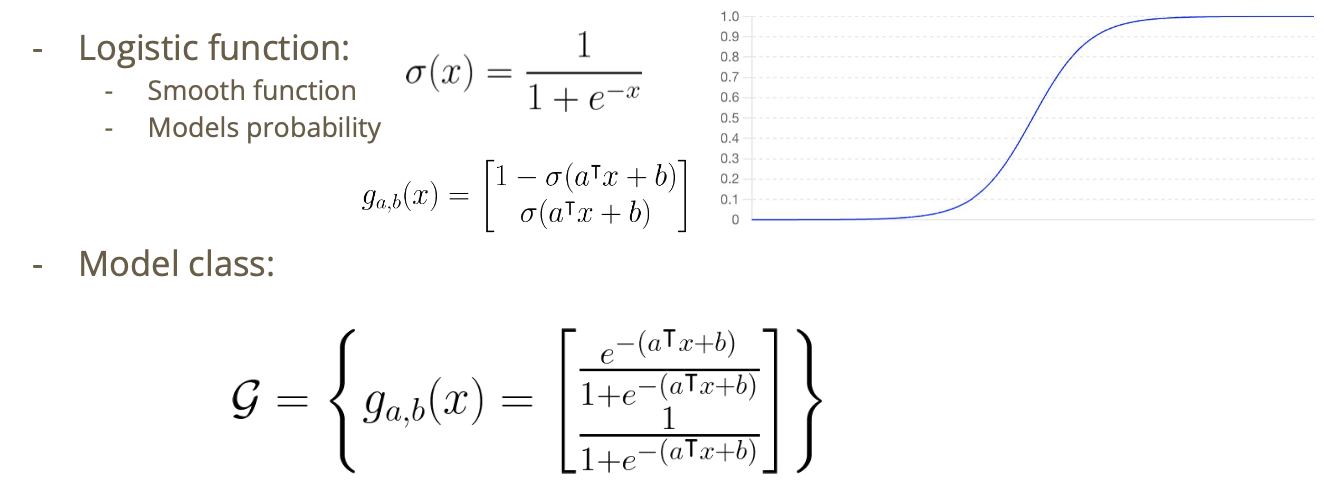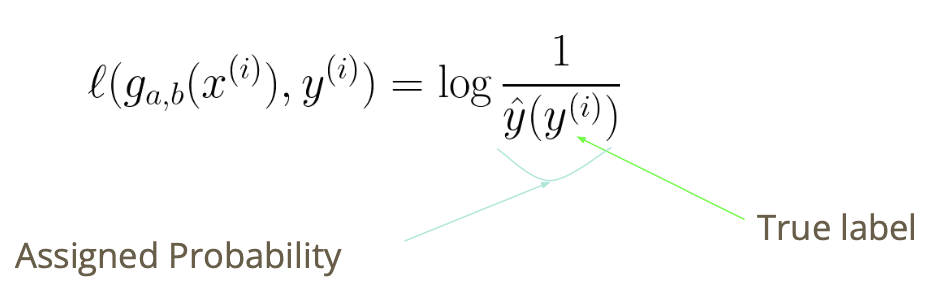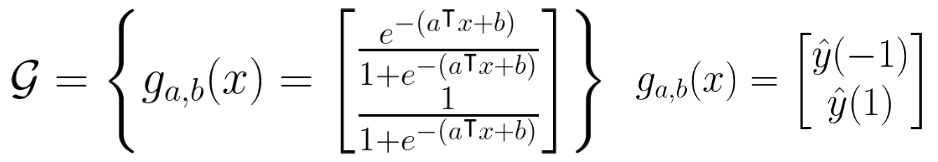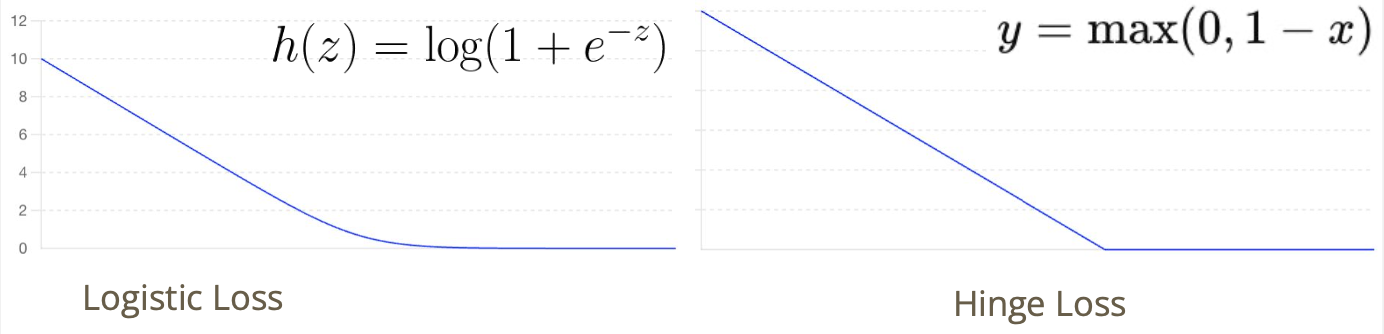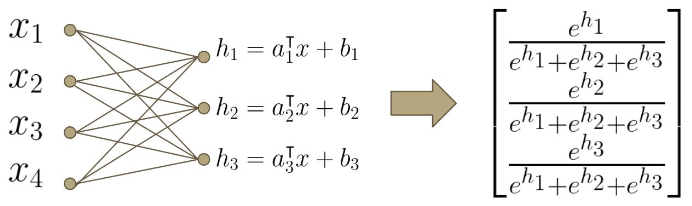[LG Aimers] [지도학습-5] Logistic Regression

Soft Guess

• 확률 기반의 예측을 제공하는 것

• Hard guess

  $g_{\theta}(x^{(i)}) = {1, -1}$

• Soft guess

  $g_\theta(x^{(i)}) = \begin{bmatrix}Pr(y^{(i)} = -1) \Pr(y^{(i)} = 1)\end{bmatrix}$

• 예: 70%의 확률로 비가 온다

Logistic Regression: Model Class

• 내 모델이 생각하는 -1인 확률과 1인 확률이 output
• 분류 문제를 회귀 문제로 바꿔서 푼다고도 해석 가능
• $a^Tx+b$가 0보다 얼마나 크거나 작은지에 따라 신뢰도가 바뀜

Cross Entropy Loss

• 따라서 출력값을 패널티화할 필요가 있음
  • 예를 들어, 비가 올 확률을 70%로 예측했는데 실제로 비가 올 경우
  • 비가 올 확률을 30%로 예측했는데 실제로 비가 오는 경우
• 사건에 더 높은 확률을 할당하면 손실값이 낮아야 함

Logistic Regression

• 데이터셋 (with binary label)

  $(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(n)},y^{(n)})$

• 함수 클래스

  

• 손실 함수

  $\ell(g_{a,b}(x^{(i)}), y^{(i)}) = \log\left(\frac{1}{\hat{y}(y^{(i)})}\right)$

Loss function

• 식을 위와 같이 정리하면, 결국 Logistic Loss는 Hinge Loss의 미분 가능한 형태라고 볼 수도 있음

Multiclass Classification

• Multiclass Classifcation은 Binary Classification을 여러번 반복해서 풀 수도 있음
• 또는 Softmax를 사용해 Label에 대한 확률 분포를 반환할 수 있음

Softmax Function

• 로지스틱 함수의 일반화

  \[z = [z_1, z_2, \ldots, z_K]\newline \sigma(z)_i = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}\]

• Output 값들은 양수이며, 다 더할 시 1이 됨

Softmax Regression

• 데이터셋 (with discrete label)

  $(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(n)},y^{(n)})$

• 함수 클래스

  

• 손실 함수

  $\ell(g_{a,b}(x^{(i)}), y^{(i)}) = \log\left(\frac{1}{\hat{y}(y^{(i)})}\right)$

False Positive, False Negative

• 임계치가 반드시 0.5일 필요는 없음
  • 애플리케이션마다 적절히 한계점을 설정하는 것이 중요함
• 예) 코로나 테스트
  • false negative보다 false positive를 선호함

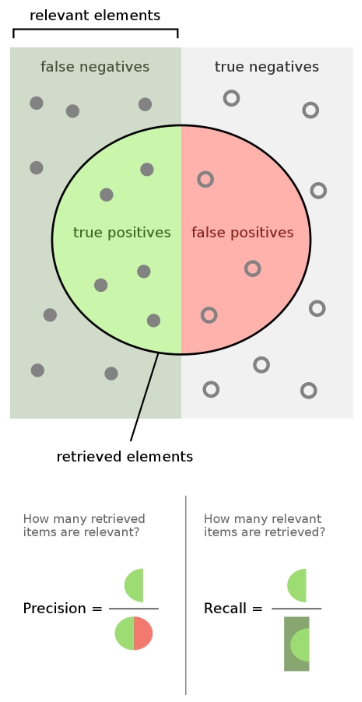
Precision and Recall

• $\mathrm{Precision} = \frac{tp}{tp+fp}$
• $\mathrm{Recall} = \frac{tp}{tp + fn}$
• Precision과 Recall에는 Trade-off 관계가 있음
• 어떤 것을 선호할지는 애플리케이션에 따라 다름
• F1-score
  • Precision과 Recall의 조화 평균

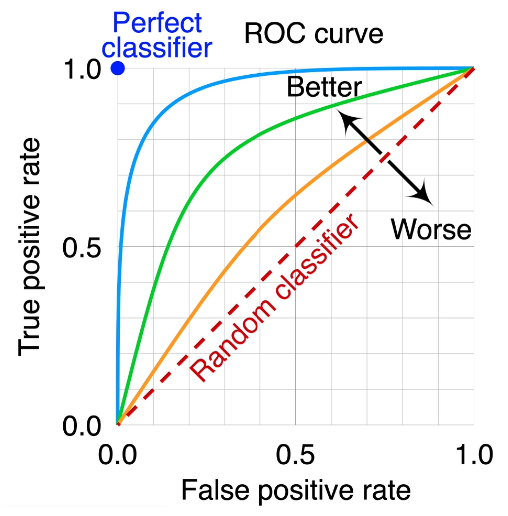
Precision, Recall, and ROC curve

• True positive rate(TPR)
  • TP/(TP+FN)
• False positive rate(FPR)
  • FP/(FP+TN)
• 언제나 positive라고 대답하는 경우
  • FN=TN=0, TPR=FPR=1
• 언제나 negative라고 대답하는 경우
  • TP=FP=0, TPR=FPR=0
• ROC curve 아래의 면적이 넓을수록, 더 좋은 classifier