[프로그래머스] [Level 3] 연속 펄스 부분 수열의 합 (C++)

문제 설명

어떤 수열의 연속 부분 수열에 같은 길이의 펄스 수열을 각 원소끼리 곱하여 연속 펄스 부분 수열을 만들려 합니다. 펄스 수열이란 [1, -1, 1, -1 …] 또는 [-1, 1, -1, 1 …] 과 같이 1 또는 -1로 시작하면서 1과 -1이 번갈아 나오는 수열입니다.

예를 들어 수열 [2, 3, -6, 1, 3, -1, 2, 4]의 연속 부분 수열 [3, -6, 1]에 펄스 수열 [1, -1, 1]을 곱하면 연속 펄스 부분수열은 [3, 6, 1]이 됩니다. 또 다른 예시로 연속 부분 수열 [3, -1, 2, 4]에 펄스 수열 [-1, 1, -1, 1]을 곱하면 연속 펄스 부분수열은 [-3, -1, -2, 4]이 됩니다.

정수 수열 sequence가 매개변수로 주어질 때, 연속 펄스 부분 수열의 합 중 가장 큰 것을 return 하도록 solution 함수를 완성해주세요.

제한 사항

• 1 ≤ sequence의 길이 ≤ 500,000
• 100,000 ≤ sequence의 원소 ≤ 100,000
  • sequence의 원소는 정수입니다.

입출력 예

sequence	result
[2, 3, -6, 1, 3, -1, 2, 4]	10

주어진 수열의 연속 부분 수열 [3, -6, 1]에 펄스 수열 [1, -1, 1]을 곱하여 연속 펄스 부분 수열 [3, 6, 1]을 얻을 수 있고 그 합은 10으로서 가장 큽니다.

---

✅ 풀이

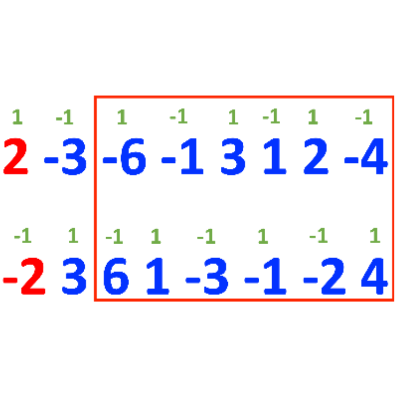
연속 부분 수열이 몇번째 인덱스에서 시작하던 간에, 위 사진과 같이 결국 모두 sequnce 배열에 1과 -1을 번갈아 가며 곱한 배열의 부분 수열로 표현이 된다는 점이 핵심이다.

결국 이 문제는 위 두 배열을 이용해 가장 큰 부분 수열의 합을 구하면 된다.

가장 큰 부분 수열의 합을 구하기 위해서 DP를 이용해 해결할 수 있는데, DP[k]를 k번째 원소까지 탐색했을 때의 최댓값이라고 하면,

\[DP[k] = max(DP[k-1]+seq[k], seq[k])\]

로 표현이 가능하다. 여기서 DP[k - 1] + seq[k]는 이전 인덱스까지의 최댓값에서 현재 seq 값을 추가로 더한 것이고, seq[k]는 부분 수열의 합이 k번 인덱스부터 시작한다고 상정한 값이다.

전체 코드는 아래와 같다.

#include <string>
#include <vector>
#include <algorithm>
#include <cmath>

using namespace std;

vector<int> purse(vector<int> v, int num) {
    for(int i = 0; i < v.size(); i++) {
        v[i] = v[i] * num;
        num *= -1;
    }

    return v;
}

long long solution(vector<int> sequence) {
    long long answer = 0;
    vector<int> seq1 = purse(sequence, 1); // [1, -1, 1, -1 ...] 펄스 수열이 적용된 경우
    vector<int> seq2 = purse(sequence, -1); // [-1, 1, -1, 1 ...] 펄스 수열이 적용된 경우
    long long DP1[500001]; // seq1에서 인덱스 i번째 원소까지 탐색했을 때의 최댓값
    long long DP2[500001]; // seq2에서 인덱스 i번째 원소까지 탐색했을 때의 최댓값

    DP1[0] = (long long)seq1[0];
    DP2[0] = (long long)seq2[0];

    for(int i = 1; i < seq1.size(); i++) {
        DP1[i] = max(DP1[i - 1] + (long long)seq1[i], (long long)seq1[i]);

        answer = max(answer, DP1[i]);
    }

    for(int i = 1; i < seq2.size(); i++) {
        DP2[i] = max(DP2[i - 1] + (long long)seq2[i], (long long)seq2[i]);

        answer = max(answer, DP2[i]);
    }

    if(sequence.size() == 1) {
        answer = abs(sequence[0]);
    }

    return answer;
}